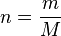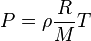Ideal gas law
The
ideal gas law is the equation of state of a hypothetical
ideal gas. It was first stated by Émile Clapeyron in 1834 as a combination of
Boyle's law and
Charles's law.
Equation
The state of an amount of gas is determined by its
pressure, volume, and
temperature. The modern form of the equation relates these simply in two main forms. The
temperature used in the equation of state is an absolute temperature: in the SI system of units, Kelvin.
Common form:
The ideal gas law is often introduced in its common form:
PV=nRT
where:
P is the
pressure of the gas
V is the volume of the gas
n is the amount of substance of gas (also known as number of moles)
R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant = 8.3145 J/mol K.
T is the
temperature of the gas
In SI units, P is measured in pascals, V is measured in cubic metres, n is measured in moles, and T in kelvin (273.15 kelvin = 0.00 degrees Celsius). R has the value 8.314 J·K−1·mol−1 or 0.08206 L·atm·mol−1·K−1or ≈2 calories if using
pressure in standard atmospheres (atm) instead of pascals, and volume in liters instead of cubic metres.
Molar form:
How much gas is present could be specified by giving the mass instead of the chemical amount of gas. Therefore, an alternative form of the
ideal gas law may be useful. The chemical amount (n) (in moles) is equal to the mass (m) (in grams) divided by the molar mass (M) (in grams per mole):
By replacing n with
m / M, and subsequently introducing density
ρ = m/V, we get:

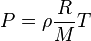
Defining the specific gas constant
Rspecific as the ratio R/M,

This form of the
ideal gas law is very useful because it links
pressure, density, and
temperature in a unique formula independent of the quantity of the considered gas. Alternatively, the law may be written in terms of the specific volume v, the reciprocal of density, as

It is common, especially in engineering applications, to represent the specific gas constant by the symbol R. In such cases, the universal gas constant is usually given a different symbol such as R to distinguish it. In any case, the context and/or units of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to.
The table below essentially simplifies the
ideal gas equation for a particular processes, thus making this equation easier to solve using numerical methods.
| Process | Constant | Known ratio | P2 | V2 | T2 |
|---|
| Isobaric process |
Pressure
|
V2/V1
| P2 = P1 | V2 = V1(V2/V1) | T2 = T1(V2/V1) |
|
T2/T1
| P2 = P1 | V2 = V1(T2/T1) | T2 = T1(T2/T1) |
Isochoric process
(Isovolumetric process)
(Isometric process) |
Volume
|
P2/P1
| P2 = P1(P2/P1) | V2 = V1 | T2 = T1(P2/P1) |
|
T2/T1
| P2 = P1(T2/T1) | V2 = V1 | T2 = T1(T2/T1) |
| Isothermal process |
Temperature
|
P2/P1
| P2 = P1(P2/P1) | V2 = V1/(P2/P1) | T2 = T1 |
|
V2/V1
| P2 = P1/(V2/V1) | V2 = V1(V2/V1) | T2 = T1 |
Isentropic process
(Reversible adiabatic process) |
Entropy
|
P2/P1
| P2 = P1(P2/P1) | V2 = V1(P2/P1)(−1/γ) | T2 = T1(P2/P1)(γ − 1)/γ |
|
V2/V1
| P2 = P1(V2/V1)−γ | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − γ) |
|
T2/T1
| P2 = P1(T2/T1)γ/(γ − 1) | V2 = V1(T2/T1)1/(1 − γ) | T2 = T1(T2/T1) |
| Polytropic process |
P Vn
|
P2/P1
| P2 = P1(P2/P1) | V2 = V1(P2/P1)(-1/n) | T2 = T1(P2/P1)(n - 1)/n |
|
V2/V1
| P2 = P1(V2/V1)−n | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1−n) |
|
T2/T1
| P2 = P1(T2/T1)n/(n − 1) | V2 = V1(T2/T1)1/(1 − n) | T2 = T1(T2/T1) |
|
|
|
|
|
|
|---|
In an isentropic process, system entropy (S) is constant. Under these conditions, P1 V1γ = P2 V2γ, where γ is defined as the heat capacity ratio, which is constant for an
ideal gas. The value used for γ is typically 1.4 for diatomic gases like nitrogen (N2) and oxygen (O2), (and air, which is 99% diatomic). Also γ is typically 1.6 for monatomic gases like the noble gases helium (He), and argon (Ar). In internal combustion engines γ varies between 1.35 and 1.15, depending on constitution gases and
temperature